Our current election system is a piece of crap. It is a hodgepodge of manual and batch systems ripe with fraud. That an online real time election system has not been made available by now is an absolute crime. So what would an online real time election system look like?
THE DATABASE:
We start with the actual database? What is a database, you ask?
It is a filing organization and access system.
Here is a diagram of what it would look like.
(Too small? On your phone, expand it. On your computer, right click and open image in new tab.)
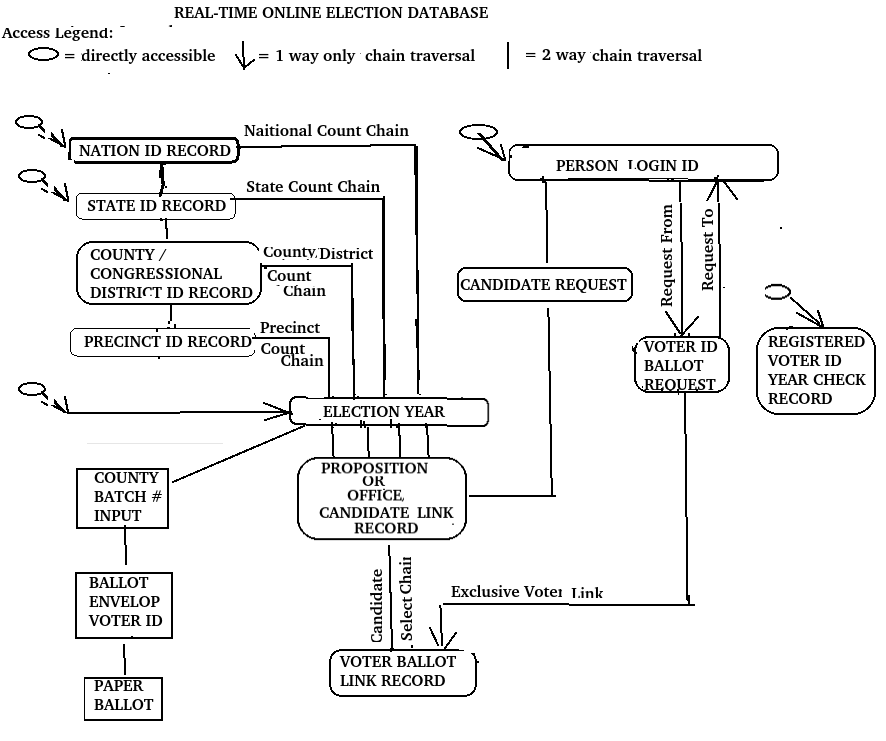
So how does one read this diagram?
Each box represents a “record type” having a specific data content & format different from the other boxes that represent different “record types”. (Note: the word “record type” is used interchangeably with the word “record”). Boxes at the top are basic entity record types & accessible via their ids. Unconnected diagonal lines into some of these top boxes indicates they are directly accessible. As you can see, there are 4 basic entity record types: year, nation, state, & person.
Lines connecting top level boxes to lower level boxes are links from top level records to lower level record types, thus forming a chain of lower level records. The top level box is said to be the master record type of the lower level detail boxes. For each top level master record there can be any number of lower level detail records.
So for example, given a nation id of USA, one could directly access the USA record & then traverse the state chain to access all the states within the USA. Similarly, one could access all the counties within a state by traversing the county chain. And so on.
Although the default direction of traversal from master to detail records appears to be downward (or forward), upward (or backward) traversal from any detail to master can be possible before a person actually votes. However after vote occurs, traversal in either direction between a voter-ballot-link record and a voter-location-link record should be restricted to the voter for privacy reasons. Today’s average browser-to-website user should not find this method of navigation too difficult to understand.
PRE-ELECTION RECORD CREATION AND MAINTENANCE RESPONSIBILITIES:
Each state would have this database file system accessible to the public via their website on their own computer. The database would be initialized only one time with the geographic records of nation, state and counties, these being fixed entities. But before participating in an election, each state resident voter, including state & county employees, must already have or create their own reusable logon id record. Only state & county employee logons should be allowed to update the entire database for the purposes of setting up the database content.
VOTER REGISTRATION & JOINING AN ELECTION:
Of particular importance before each election is the validation and creation of the voter-ballot-link records for each logon record. This process establishes the voter rolls for each specific election. It begins with a person submitting a voter-id-ballot-request record to an authorized state employee who initiates a search of other states by checking each states registered-voter-year-check record. If no such record is found & everything else checks out on the person, the state employee creates a single year-voter check record, followed by setting up the voter-ballot-link records leaving blank the candidate-selection button in each voter-ballot-link record.
VOTING:
The database is now ready for the voter to make his candidate selections by clicking the appropriate candidate-selection button in each appropriate voter-ballot-link record, at which time a write-permission lock is placed on the voter-ballot-link record. This would prevent anyone from changing candidate-selection button and the corresponding link to the selected candidate record.
POST VOTING RECORD ACCESS:
For secrecy/privacy purposes all cast voter-ballot-link records should be locked from updating by anyone other than the voter and as soon as they are counted. With this one exception, all should be able to view any record at any time, thus providing complete transparency and veracity of an election.
In other words, everyone can look anywhere but not touch.
THE NETWORK:
Each state would have the same file system within a website on their own computer. In addition to state residents being able to create and logons to the state website, each state computer would have access to other state computers to eliminate double dipping voters who might try to vote in more than one state. Currency of voter rolls is essential.
In addition, currency of vote tabulation is essential. As soon as a voter has locked his voter-ballot record, his vote should be counted and tallies by candidate should be made available. Washington DC should be connected to each state & have access to each state database for the purpose of rolling up ballot totals for each national candidate by state.
PROS:
What would be the advantages of an online real time election system?
First, the voter would cast his ballot directly into the database, thereby eliminating anybody other than the voter from touching his ballot.
Second, the election should be completed within 2 days.
Third. since there is only one machine per state involved, auditing software should be comparatively easy as well as identifying any other anomalies.
CONS:
There will always be some ding dong who insists on having a paper ballot which necessitates having a batch input system.

