Category: TECH
Our current election system is a piece of crap. It is a hodgepodge of manual and batch systems ripe with fraud. That an online real time election system has not been made available by now is an absolute crime. So what would an online real time election system look like?
THE DATABASE:
We start with the actual database? What is a database, you ask?
It is a filing organization and access system.
Here is a diagram of what it would look like.
(Too small? On your phone, expand it. On your computer, right click and open image in new tab.)
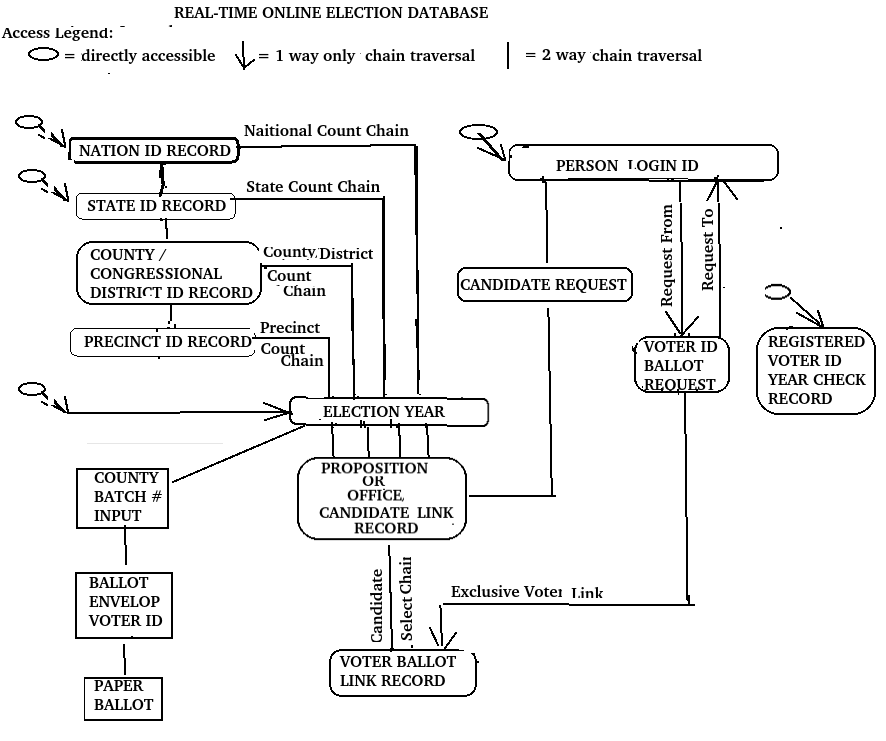
So how does one read this diagram?
Each box represents a “record type” having a specific data content & format different from the other boxes that represent different “record types”. (Note: the word “record type” is used interchangeably with the word “record”). Boxes at the top are basic entity record types & accessible via their ids. Unconnected diagonal lines into some of these top boxes indicates they are directly accessible. As you can see, there are 4 basic entity record types: year, nation, state, & person.
Lines connecting top level boxes to lower level boxes are links from top level records to lower level record types, thus forming a chain of lower level records. The top level box is said to be the master record type of the lower level detail boxes. For each top level master record there can be any number of lower level detail records.
So for example, given a nation id of USA, one could directly access the USA record & then traverse the state chain to access all the states within the USA. Similarly, one could access all the counties within a state by traversing the county chain. And so on.
Although the default direction of traversal from master to detail records appears to be downward (or forward), upward (or backward) traversal from any detail to master can be possible before a person actually votes. However after vote occurs, traversal in either direction between a voter-ballot-link record and a voter-location-link record should be restricted to the voter for privacy reasons. Today’s average browser-to-website user should not find this method of navigation too difficult to understand.
PRE-ELECTION RECORD CREATION AND MAINTENANCE RESPONSIBILITIES:
Each state would have this database file system accessible to the public via their website on their own computer. The database would be initialized only one time with the geographic records of nation, state and counties, these being fixed entities. But before participating in an election, each state resident voter, including state & county employees, must already have or create their own reusable logon id record. Only state & county employee logons should be allowed to update the entire database for the purposes of setting up the database content.
VOTER REGISTRATION & JOINING AN ELECTION:
Of particular importance before each election is the validation and creation of the voter-ballot-link records for each logon record. This process establishes the voter rolls for each specific election. It begins with a person submitting a voter-id-ballot-request record to an authorized state employee who initiates a search of other states by checking each states registered-voter-year-check record. If no such record is found & everything else checks out on the person, the state employee creates a single year-voter check record, followed by setting up the voter-ballot-link records leaving blank the candidate-selection button in each voter-ballot-link record.
VOTING:
The database is now ready for the voter to make his candidate selections by clicking the appropriate candidate-selection button in each appropriate voter-ballot-link record, at which time a write-permission lock is placed on the voter-ballot-link record. This would prevent anyone from changing candidate-selection button and the corresponding link to the selected candidate record.
POST VOTING RECORD ACCESS:
For secrecy/privacy purposes all cast voter-ballot-link records should be locked from updating by anyone other than the voter and as soon as they are counted. With this one exception, all should be able to view any record at any time, thus providing complete transparency and veracity of an election. In other words, everyone can look anywhere but not touch.
THE NETWORK:
Each state would have the same file system within a website on their own computer. In addition to state residents being able to create and logons to the state website, each state computer would have access to other state computers to eliminate double dipping voters who might try to vote in more than one state. Currency of voter rolls is essential.
In addition, currency of vote tabulation is essential. As soon as a voter has locked his voter-ballot record, his vote should be counted and tallies by candidate should be made available. Washington DC should be connected to each state & have access to each state database for the purpose of rolling up ballot totals for each national candidate by state.
PROS:
What would be the advantages of an online real time election system?
First, the voter would cast his ballot directly into the database, thereby eliminating anybody other than the voter from touching his ballot.
Second, the election should be completed within 2 days.
Third. since there is only one machine per state involved, auditing software should be comparatively easy as well as identifying any other anomalies.
CONS:
There will always be some ding dong who insists on having a paper ballot which necessitates having a batch input system.
INTERNET BASICS
Rules For Securing Your Own Email:
1. You can’t secure your email if you use a cloud email service except via the tools provided by the email service
2. Your router and your firewall are all you need to secure your own email server. This requires a simple understanding of how internet addressing works.
First, understand that a domain name has no real significance in addressing. All addressing boils down to an IP NUMBER and a PORT NUMBER. The ip number, v.w.x.y, is the equivalent of a building address. The port number, z, is the equivalent of an apartment number. The two are expressed together as v.w.x.y :z.
With respect to email, the port numbers 25 and 587 are used to send email. The port numbers 143 and 993 are used to retrieve email in an IMAP fashion as opposed to 110 and 995 in a POP fashion.
So how do I block out unwanted hackers or spammers. First, my ROUTER must block out all unused ports, ie, empty apartment numbers. But it has to let through all traffic to the ports in use, ie, ports 25 and 587. This is accomplished via PORT FORWARDING, which is a function in your router to direct traffic addressing a port to its ultimate computer program, ie, destination.
Secondly, I have to use the firewall to block out the ip numbers (addresses) of unwanted visitors trying to hack my computer. These are found by inspecting the email server log. The hackers become quite obvious in the log.
Oh, wondering about my ip address? It is the ip assigned to me by my internet service provider. The isp forwards all internet traffic calling out this ip address to my router which begins sorting out what ports go to what computers I have on my local network.
What is my local network? That’s everything I have wifi-ed or physically attached to my router. And how do ports get connected to programs? Once the router directs a specific port to a specific computer, the programs (apps) have to be told what ports to “LISTEN” to.
So what has domain naming got to do with anything? First, we have to know that a domain is a fancy word to identify the digital hardware and software resources belonging to a specific owner. So I have two main domains that are identified as trcooper.com and aaarrrg.com. These names get resolved (translated) into the ip addresses where they reside(hosted) by an INTERNET DOMAIN NAME SERVER (DNS) which is nothing more than a lookup service, like a phone book or 411.
So, getting back to the actual residency of my domains, the trcooper.com main domain is on the GoDaddy computers, whereas aaarrrg.com is on my home computer. These are where my websites reside.
But what about my email server? Where does it reside? This is where SUB-DOMAIN naming comes in. My email server resides on my home computer which is identified as a sub-domain of trcooper.com and identified as mail.trcooper.com. The dns server will direct all traffic calling out mail.trcooper.com to my home computer and not the GoDaddy computer. So it’s all like a company that has multiple addresses.
The only thing I have not covered is encryption which provides the ultimate security in digital communication. Another word that goes flying around is the word “protocol”. I find this word being so widely abused that it has almost lost its meaning. Basically, it is a predefined way in which two communicants can verify they are speaking to the right person. One of the first protocols was the “ack”- “nak” , acknowledge- no acknowledge. Different strokes for different folks. Ground control to major Tom. At the current time, it appears as though a protocol called TLS (transport layer security) is replacing SSL (secured socket layer) in two-way digital communications.
A. THE MEANING OF DIRECTION & SIGNAGE:
We humans see ourselves in terms of position: vertical upright,
horizontal on back, & horizontal on side. These being our most
common positions relative to Earth, they become the 3 basic
dimensions that are seen as 3 linear axes orthogonal (at right
angles) to each other. Furthermore, we think of measurable
increments along each axis as being in the positive or negative
direction depending upon their position relative to a zero point
on the axis. Such a concept gives us a 3-dimensional reference
system that we see as absolute, albeit not necessarily so.
In mathematics unfortunately the plus and minus signs have two
different meanings, depending upon the position relative to an
operand. When touching an operand, it means the value of the
operand is in the positive or negative direction along a linear axis.
But it can also mean to add or subtract the operand in the absence
of an explicit operator between two numbers. And in the absence
of a touching sign, the default is in the positive direction. When
not touching an operand, it means addition or subtraction
between two operands, ie, it becomes an operator. So in an
expression, there can be both directional signs and operational
signs.
As a side note & not relevant to this discussion, a minus sign in
front of an exponent means to raise the reciprocal of the base to
the power indicated by the exponent.
B. IMAGINARY NUMBERS:
The imaginary number, i, is said to be the square root of -1 which
is impossible, because according to current convention, there is no
number multiplied by itself one time that yields a negative number.
Lacking the ability to determine a numeric value, the square root
of -1 is assigned the variable, “i” & complex numbers are
mathematical expressions containing “i”. A complex number is of
the form (+or-)a + (+or-)b * i, where “a” is the numerical offset,
“b” is the numerical multiplicand, & “i” is the Multiplier. It is rare
to see i * b, where “i”, as the Multiplier, precedes “b”, as the
multiplicand. But that is going to change in this writing, as we
shall soon see.
C. THE RULES OF MULTIPLICATION:
The aforementioned indeterminate problem of not being able to
evaluate “i” arises from the fact that mathematicians established
long ago that A MINUS NUMBER TIMES A MINUS
NUMBER SHOULD BE POSITIVE. Furthermore, they
established that THE PRODUCT OF TWO OPPOSITELY
SIGNED VALUES SHOULD BE NEGATIVE. These
conclusions arose due to the distributive law of mathematics.
Let me state here my belief that when it comes to groupings
via ( ..), the order of operations should dictate that expressions
within a group should be evaluated first. But I will not quibble
over the distributive law.
D. CURRENT MULTIPLY OPERATIONS IN USE:
These current-day conventions affecting a change in value
resulting from multiplication can be expressed as follows:
Let:
M = multiplier/operator
m = multiplicand/operand
“*” means times,
(not to be confused with “**” which means exponent of)
R = resulting product
1. THE PRODUCTS OF ACCUMULATIVE
MULTIPLICATION:
Accumulation Of Positives:
Plus times Plus = Plus
+M * +m = +R
Interpretation:
Add +m to the current value M times.
OR GRAPHICALLY,
Relative to the current point,
go right M times in increments of |m|.
Example:
+3 * +2 = +2 + 2 + 2 = 6
Accumulation Of Negatives:
Plus times Minus = Minus
+M * -m = -R
Interpretation:
Add -m to current value M times.
OR GRAPHICALLY,
Relative to the current point,
go left M times in increments of |m|.
Example:
+3 * -2 = 0 + ( – 2 – 2 – 2)
= 0 + – ( 2 + 2 + 2) = -6
2. THE PRODUCTS OF DECUMULATIVE
MULTIPLICATION:
Decumulation Of Positives:
Minus times Plus = Minus
-M * +m = -R
Interpretation:
Subtract +m from the current value M times..
OR GRAPHICALLY,
Relative to the current point,
go left M times in increments of |m|.
Example:
-3 * +2 = 0 + -( 2 + 2 + 2) = – 6
Decumulation Of Negatives:
Minus times Minus = Plus
-M * -m = +R
Interpretation:
Subtract -m from current value M times.
OR GRAPHICALLY,
Relative to the current point,
go right M times in increments of |m|.
Example:
-3 * -2 = – ( -2) – (-2) – (-2 )
= + 2 + 2 +2 = +6
Observe that I have identified two different types of multiplication,
“accumulative” and “decumulative”. I make this distinction
because accumulative multiplication requires repetitive addition,
where decumulative multiplication requires repetitive subtraction.
Also, we note that the sign of the product resulting from the
repetitive multiplication of a negative multiplicand alternates
between + on even repetitions & – on odd repetitions. In other
words, a successive number of subtractions of a negative number
from itself ALTERNATES BETWEEN + & -. This alternation
does not appear anywhere else. So this behavior is seen as
unusual.
E. RECONSTRUCTING THE PICTURE OF MULTIPLICATION:
By insisting that the Multiplier always occurs in front of the
multiplicand, we can clearly see that, among other things, a
negative Multiplier means decumulation, whereas a positive
Multiplier means accumulation. Aside from this fact, we might
speculate that there could be other meanings in addition. What
those could be, we are about to find out.
Moving on, we might assert that the Multiplier,M, reside on an
M-axis different from the multiplicand,m, on a separate m-axis,
with the two axes intersecting each other orthogonally at right
angles. So the visual graphic of the Multiplier in relation to the
multiplicand becomes a 2-dimensional planar picture with each
axis having its own set of + & – directions, rather than just a
simple 1-dimensional linear graphic.
THIS NOT JUST THIS
m-axis
| +
– ——0——- + M-axis – ———0———+ M & m
| – (We are not just talking candy here)
Given this distinction, we can now begin to think in terms of:
VECTOR CROSS-MULTIPLICATION,
(aka, CROSS-MULTIPLICATION
or
CROSS-COMPUTATION
or
X-MULTIPLICATION) ,
versus
VECTOR DOT-MULTIPLICATION,
(aka, DOT-MULTIPLICATION
or
DOT-COMPUTATION
or
*-MULTIPLICATION
or
SCALAR-MULTIPLICATION) .
The difference is as follows.
Vector dot multiplication results in a simple 1-dimensional product
(called the dot-product) that resides on the same axis as the
Multiplier & multiplicand. Up to now, current conventional
multiplication has always been equivalent to vector dot
multiplication for both accumulative and decumulative
multiplication. But that is about to change, as we are about to
change decumulative multiplication from vector dot to vector
cross multiplication. The mathematical expression for computing
the vector cross product is given as:
R = M * m
Vector cross multiplication results in a product (called the
cross-product) that is uniquely identified with a direction which
is orthogonal to directions identified by the M-axis & the m-axis.,
& whose numerical value is the simple product of the two
numerical values further multiplied by the sine of the smallest
angle, @, between the two vectors, M and m. The mathematical
expression for computing the vector cross product is given as:
R = M X m = M * m* sine(@) .
So we now have two methods of multiplication, with
cross-multiplication giving us a clearer 3-dimensional/directional
picture shown as follows.
+ m-axis + R-axis = CROSS PRODUCT AXIS
^ /\
| ‘
| ‘
| R1 = (M1 X m1) * sine(90) /
m1 ‘
| ‘
-M————–0———— M1 ——–> + M-axis
‘ | @ = -90
‘ |
‘ |
‘ |
-R -m
We now proceed to examine the deeper meanings of the
cross-multiplication method.
F. ABOUT THE ANGLE, @, BETWEEN M & m.
We’ve started out saying that M-axis was orthogonal to
m-axis for the sake of simplicity. But the cross-product
approach says that such is not always the case when it comes
to vectors, because @ can take on any value between +90
degrees and -90 degrees as the shortest path between the
sides of the angle. And this has consequences for both the
numerical value of the resultant, R, its dimension & its
positive versus negative directions.
Before we go any further, we need to have a clear understanding
of how we view angles from a fixed observation point. Then we
need to know what the sine of an angle is. And finally, we can
discuss what role the of the angle between the Multiplier &
multiplicand might be.
1. ABOUT PLUS & MINUS ANGLES:
Envision the face of your clock where the M-axis is a straight
line running from 12 to 6 in a negative direction & the m-axis
is a straight line running from 9 to 3 in a positive direction.
Progressing clockwise, we consider 12 o’clock to be +0
degrees, & relative to it we recon 3 o’clock to be +90 degrees,
6 o’clock to be +180 degrees, & 9 o’clock to be +270 degrees.
But progressing counter-clockwise from 12 o’clock, we
consider +270 degrees to be -90 degrees & +180 degrees
to be -0 degrees. So in this scenario, 12 o’clock is the reference
side of any angle from it. And because we have aligned the
M-axis with 12 o’clock, the M-axis is also the reference side
of any angle at which the m-axis intersects it. Furthermore,
should the M-axis be in a direction other than 12 o’clock,
then the M-axis should remain the reference side of the
angle, @.
Therefore, the plus or minus direction of the angle,@, between
the M-axis and the m-axis depends upon whether or not we go
clockwise or counterclockwise from the M-axis to the m-axis.
And the shortest path from M to m will dictate whether we
proceed clockwise or counterclockwise from M.
2. ABOUT THE SINE OF AN ANGLE:
Now what about the sine of @? Without going into too much
detail about what is meant by the sine of an angle, it is enough
to say that the sine( +0 degrees) is +0, the sine(+90 degrees) is
+1, the sine(-0 degrees) is -0, & the sine(-90 degrees) is -1.
So the sine of an angle acquires the same sign as the sign of the
angle. If the angle is negative, its sine is negative. If the angle is
positive, its sine is positive.
3. WHICH WAY JOSE, PLUS OR MINUS?:
We now have to determine in what direction the product
points, plus or minus, along the resulting orthogonal axis.
Traditional vector math calls for the application of the RIGHT
HAND THUMB RULE. Finding this to be a little too
nebulous to explain, I will only mention that the index
finger should be the multiplicand. I leave it there.
As an option, I would suggest discounting the sign of the
Multiplier and applying the sign arising from the sine(@)
to the sign of the multiplicand to determine the sign of the
resultant.
G. REDEFINING ACCUMULATIVE VS DECUMULATIVE
CROSS-MULTIPLICATION:
Having identified two different, but similar forms of
multiplication, we now ask,”Are we using the correct form
of multiplication for each?”. After all, we see some unexplainable
differences between decumulative & accumulative operations.
So let’s try applying vector cross-computation to multiplication
instead of dot-computation.
We can now see that cross-multiplication not only results
in a product pointing in an orthogonal direction away from
the directions of the Multiplier & multiplicand, but can
yield an absolute value entirely different from today’s
conventional multiplication, especially if the sine(@) is
other than +1 or -1. Therefore, we ask “Which value(s)
+1 or -1 would yield the same results as todays
multiplication”.
The answer(s) are clear. For accumulative
multiplication, we need a sine(@) = +1, ie, @ = +90.
For decumulative multiplication we need sine(@) = -1,
ie. @ = -90. With this understanding, we now modify the
current conventions by simply replacing the * operator with
the X operator and adding the (sine @), making @ = +90
for accumulative & @ = -90 for decunulative
multiplication.
Let:
M = multiplier/operator
m = multiplicand/operand
“*” means times,
(not to be confused with “**” which means exponent of)
“X” means vector cross multiplication,
(not to be confused with variable “x” )
“@” is the smallest angle between the M-axis & m-axis.
It is plus (+) if the shortest distance
from the M-axis to the m-axis is clockwise.
It is minus (-) if counterclockwise.
R = resulting product
1. ACCUMULATIVE CROSS-MULTIPLICATION:
For accumulative multiplication, +90 degrees is appropriate.
In order for the resultant product, R, to become the same
value as determined by vector dot multiplication, the value
of sine(@) must equal +1, which means the angle, @, between
the +M-axis and +m-axis must be +90 degrees.
@ = +90, sine(+90) = +1
Accumulation Of Positives:
Plus times Plus = Plus
R = +M X (+m)
= |+M| * (+m) * sine(@)
= |+M| * (+m) * sine (+90)
= |+M| * (+m) * (+1)
= |+M| * (+m)
= + (M * m)
Accumulation Of Negatives:
Plus times Minus = Minus
R = +M X (-m)
= |+M| * (-m) * sine(@)
= |+M| * (-m) * sine (+90)
= |+M| * (-m) * (+1)
= |+M| * (-m)
= – (M * m)
2. DECUMULATIVE CROSS-MULTIPLICATION:
For decumulative multiplication, -90 degrees works.
In order for the resultant product, R, to become the same
value as determined by vector dot multiplication, the value
of sine(@) must equal -1, which means the angle, @, between
the +M-axis and +m-axis must be -90.
@ = -90, sine(-90) = -1
Decumulation Of Positives:
Minus times Plus = Minus
R = -M X (+m)
= |-M| * (+m) * sine(@)
= |-M| * (+m) * sine (-90)
= |-M| * (+m) * (-1)
= |-M| * (-m)
= – (M * m)
Decumulation Of Negatives:
Minus times Minlus = Plus
R = -M X (-m)
= |-M| * (-m) * sine(@)
= |-M| * (-m) * sine (-90)
= |-M| * (-m) * (-1)
= |-M| * (+m)
= + (M * m)
Note that I did not recognize or apply the sign of the Multiplier. It
was unnecessary when the sine(@) was included. Of course, I
could have made @ = +90 for the decumulative operation. But
then there still needed to be some explanation for the differences
from accumulative cross-multiplication.
H. THE MYSTERY OF THE FLIP-FLOPPING RESULTANT:
1. ABOUT SUCCESSIVE MULTIPLICATIONS.:
The fact that the resultant product of M1 X m1, R1, always
resides in the direction orthogonal to the plane of the M-axis/
m-axis, only one possible direction is left in which R may
reside, that direction being identified as the R-axis. And if that
resultant product, R1, now becomes the multiplicand, m2, of
a 2nd such computation involving a new M2, then the direction
of the new resultant product, R2, must be on the same axis as
the previous multiplicand, m1. And if that product, R2,
becomes the next multiplicand m3, on a 3rd such computation,
then the direction of the new resultant product, R3, must be in
the same direction as R1. In other words, given a succession
of repetitive vector cross-multiplications & where the
resulting product becomes the next multiplicand, the R-axis
switches positions with the m-axis & reverses its negative &
positive directions.
2. REPETITIVE
DECUMULATIVE CROSS-MULTIPLICATION
OF NEGATIVE REAL NUMBERS:
The placement of the product appears as a positive on the
R-axis & as a negative on the m-axis in alternating order
due to the right-hand thumb rule flip-flopping with each
iteration of computing the cross-product.
This explains why a repetitious negative times a negative
equals a positive R1 on the R-axis, followed by a negative
R2 on the m-axis, followed by a positive R3 back on the
R-axis. It gives the appearance of a pulsating R-axis
acting as a binary switch between + & -.
3. RAISING IMAGINARY -i TO THE Pth POWER.
If we conduct a succession of decumulative-cross
multiplications of -i , assuming @ = 90 degrees, we get:
(Cycle begins)
(-i)**2 = -i X -i = +i**2 = -1 ( R1 to the R-axis)
______________|
V
(-i)**3 = -i X -1 = -1 X -i = +i (R2 to the m-axis)
______________|
V
(-i)**4 = -i X +i = +1 (R3 to the R-axis?)
______________|
V
(-i)**5 = -i X +1 = -i ( R4 to the m-axis?)
|
(Cycle starts over) |
_______________|
V
(-i)**6 = -i X -i = -1 (R5 to the R-axis?)
Powers of (-i) confirmed by internet.
Of great interest here is the observation that the successive
multiplications oscillate between real rational numbers and
imaginary irrational + & – i. We must ask, ” is i the basic
unit of measure in the world of irrational numbers?”.
NOTE: e**i*pi = -1 where e is Eulers irrational constant.
I. CONCLUSIONS:
1. We have identified two distinct forms of multiplication, ie,
accumulative vs decumulative multiplication, the difference
being the accumulative form is a series of additions whereas
the decumulative form is a series of subtractions.
The sign of the Multiplier, M, identifies which form it is.
2. We have identified two methods of multiplication, dot-product
multiplication and cross-product multiplication, We have
adopted cross-product as the proper method to be used in both
accumulative and decumulative multiplication. In doing so,
we recognize the angle between between the Multiplier &
multiplicand to be +90 degrees for accumulative multiplication
as opposed to -90 degrees for decumulative multiplication.
As a result, the sign of the Multiplier does not enter into the
computation of the product.
3. The angle, @, from the Multiplier to the multiplicand is
normally +90 degrees in order to make the sine(@) = +1,
thereby confirming that the M-axis is normally orthogonal
to the m–axis, albeit not eliminating other possibilities for
values of angle @, resulting in a wide variety of product
values and plus or minus direction.
4. The fact that both operands, M & m, reside on a different axis
as vectors means that the communitive law no longer applies,
disproving the idea that a minus times a plus is the same as
a plus times a ninus. It becomes like saying
6 cats are the same as 6 dogs.
Nothing has been done to change anything outside the realm of
conventional arithmetic & mathematics. Rather we have found
old precepts to be applied in new ways to open the door to
understanding some areas that left us perplexed. As a result, we
have uncovered a new way of perceiving multiplication, resulting
in the identification of decumulative multiplication as distinct
from traditional accumulative multiplication. We have uncovered
some interesting details about how we can graphically interpret
multiplication that involves what we call “direction” Finally, we
have shed important new light on an entity that has kept its
meaning hidden from us for so long,
ie, the imaginary number, “i”.